[Do it! 알고리즘]03. 검색

업데이트: January 20, 2021
26 분 소요

03-1 검색 알고리즘

(1) 검색과 키

주소록을 검색한다고 정해 보면, 검색(searching)은 다음과 같은 과정으로 이루어진다.

1) 국적이 한국인 사람을 찾는다.
2) 나이가 21세 이상 27세 미만인 사람을 찾는다.
3) 찾으려는 이름과 가장 비슷한 이름의 사람을 찾는다.

어떤 검색을 할 때 특정 항목에 주목한다는 점은 ‘검색하기’의 공통점이다. 주목하는 항목을 키(key)라 한다.
국적을 검색하는 경우 국적이 키이고, 나이를 검색하는 경우 나이가 키이다.
데이터가 단순한 정숫값이면 데이터 값을 키 값이라고 생각해도 좋지만, 대부분의 경우에서 키는 데이터의 ‘일부’이다.
위의 검색 과정을 살펴보면 키 값을 아래처럼 지정하고 있다.

1) 키 값과 일치하도록 지정한다(한국).
2) 키 값과 구간을 지정한다(21세 이상 27세 미만).
3) 키 값과 비슷하도록 지정한다(발음이 가장 비슷한 이름).

이런 조건은 하나만 지정하기도 하지만 논리곱이나 논리합을 사용하여 복합해서 지정하기도 한다.

(2) 배열에서 검색하기

배열 검색에서는 다음의 알고리즘을 활용한다.
선형 검색 : 무작위로 늘어놓은 데이터 모임에서 검색을 수행한다.
이진 검색 : 일정한 규칙으로 늘어놓은 데이터 모임에서 아주 빠른 검색을 수행한다.
해시법 : 추가, 삭제가 자주 일어나는 데이터 모임에서 아주 빠른 검색을 수행한다.
- 체인법 : 같은 해시 값의 데이터를 선형 리스트로 연결하는 방법
- 오픈 주소법 : 데이터를 위한 해시 값이 충돌할 때 재해시하는 방법
어떤 목적을 이루기 위해 선택할 수 있는 알고리즘이 여러 가지인 경우에는 용도나 목적, 실행 속도, 자료 구조 등을 고려하여 알고리즘을 선택해야 한다.
데이터 추가 비용?
- 학생의 번호 순서대로 키(height)의 값을 넣은 배열이 있다고 가정할 경우, 학생의 번호만 알면 바로 키(height)를 찾을 수 있다. 하지만 새로운 학생 데이터를 중간에 끼워 넣어야 할 경우라면 이후의 학생을 모두 뒤로 밀어 넣는 작업을 해야 한다. 이런 경우에 ‘배열은 검색이 빠르지만 데이터를 추가하기 위한 비용이 많이 든다‘라고 한다.

03-2 선형 검색

(1) 선형 검색

요소가 직선 모양으로 늘어선 배열에서 검색은 원하는 키 값을 갖는 요소를 만날 때까지 맨 앞부터 순서대로 요소를 검색하는데, 이것을 선형 검색(linear search) 또는 순차 검색(sequential search)이라는 알고리즘이다.
키 값과 같은 값을 가진 요소가 배열에 없을 수도 있는데, 이런 경우 검색을 끝까지 수행해도 키 값과 같은 값의 요소를 만나지 못하므로 검색에 실패하기도 한다.
검색이 종료되는 조건
- 조건1) 검색할 값을 발견하지 못하고 배열의 끝을 지나간 경우
- 조건2) 검색할 값과 같은 요소를 발견한 경우
선형 검색을 구현한 프로그램을 작성한다.

package chapter03;

import java.util.Random;
import java.util.Scanner;

public class ex01 {
  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);

    System.out.print("요솟수 : ");
    int no = stdIn.nextInt();
    int[] x = new int[no];

    Random random = new Random();

    for (int i = 0; i < no; i++) {
      x[i] = random.nextInt(10);
      System.out.printf("x[%d] : %d\n" , i, x[i]);
    }

    System.out.print("검색할 값(숫자) : ");
    int key = stdIn.nextInt();

    int index = seqSearch(x, no, key);
    if (index == -1) {
      System.out.println("검색에 실패했습니다.");

    } else {
      System.out.printf("%d는 %d번째 요소입니다.", key, index);
    }

  }

  static int seqSearch(int[] a, int n, int key) {
    int i = 0;

    while (true) {
      if (i == n) {
        return -1; // 검색 실패(-1 반환)
      }
      if (a[i] == key) {
        return i; // 검색 성공(인덱스 반환)
      }
      i++;
    }
  }

}

메서드 seqSearch는 배열 a의 처음부터 끝가지 n개의 요소를 대상으로 값이 key인 요소를 선형 검색하고, 검색한 요소의 인덱스를 반환한다. 값이 key인 요소가 존재하지 않으면 -1을 반환한다.
값이 key인 요소가 여러 개 존재할 경우 반환값은 검색 과정에서 처음 발견한 요소의 인덱스가 된다.
while문을 빠져나가는 조건
- 조건1) i == n이 성립하는 경우 (검색 실패이므로 -1을 반환)
- 조건2) a[i] == key가 성립하는 경우 (검색 성공이므로 i를 반환)
배열의 검색을 while문이 아니라 for문으로 구현하면 프로그램은 더 짧고 간결해진다.

static int seqSearch(int[] a, int n, int key) {
  for (int i = 0; i < n; i++) {
    if (a[i] == key) {
      return i;
    }
  }
  return -1;
}

선형 검색은 배열에서 순서대로 검색하는 유일한 방법이다.

무한 루프

무한 루프는 무한하게 반복하는 구조로, break문이나 return문을 사용하면 루프에서 빠져나올 수 있다.
while문과 for문은 첫 번째 행만 읽어도 무한 루프인지 알 수 있다. 반면에 do문은 끝까지 읽지 않으면 무한 루프인지 아닌지 알 수 없어 do문에 의한 무한 루프 구현은 권장하지 않는다.

while(true) {

}

for( ; ; ) {

}

do {

} while(true);

(2) 보초법

선형 검색은 반복할 때마다 종료 조건을 모두 판단한다. 단순한 판단이라고 생각할 수 있지만, 매번 종료 조건을 검사하는 비용은 무시할 수 없다. 이 비용을 반(50%)으로 줄이는 방법이 보초법(sentinel method)이다.
- 종료 조건1) 검색할 값을 발견하지 못 하고 배열의 끝을 지나간 경우
- 종료 조건2) 검색할 값과 같은 요소를 발견한 경우
검색하기 전에 검색하고자 하는 키 값을 맨 끝 요소에 저장한다. 이때 저장하는 값을 보초(sentinel)라고 한다. 그러면 원하는 값이 원래의 데이터에 존재하지 않아도 보초까지 검색하면 종료 조건이 성립한다.
보초는 반복문에서 종료 판단 횟수를 2회에서 1회로 줄이는 역할을 한다. 따라서 보초법을 활용할 때는 기존의 요솟수에 1을 더한 크기의 배열을 생성한다.

package chapter03;

import java.util.Random;
import java.util.Scanner;

public class ex02 {
  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);

    System.out.print("요솟수 : ");
    int no = stdIn.nextInt();
    int[] x = new int[no + 1]; // 요솟수 + 1 크기로 배열 생성

    Random random = new Random();

    for (int i = 0; i < no; i++) {
      x[i] = random.nextInt(10);
      System.out.printf("x[%d] : %d\n" , i, x[i]);
    }

    System.out.print("검색할 값(숫자) : ");
    int key = stdIn.nextInt();

    int index = seqSearchSen(x, no, key);
    if (index == -1) {
      System.out.println("검색에 실패했습니다.");

    } else {
      System.out.printf("%d는 %d번째 요소입니다.", key, index);
    }

  }

  static int seqSearchSen(int[] a, int n, int key) {
    int i = 0;

    a[n] = key; // 보초 추가

    while (true) {
      if (a[i] == key) { // 검색 성공
        break;
      }
      i++;
    }

    return i == n ? -1 : i;
  }

} 

보초를 사용하기 전에는 두 개의 if문을 사용하였지만, 보초를 사용하고 나서는 하나의 if문을 사용한다.

if (i == n) // 종료 조건1
if (a[i] == key) // 종료 조건2

while문의 반복이 완료된 후 찾은 값이 배열의 원래 데이터인지 아니면 보초인지 판단한다. 변수 i값이 n이면 찾은 값이 보초이므로 검색 실패임을 나타내는 -1을 반환한다.

03-2 이진 검색

(1) 이진 검색

이진 검색(binary search)은 요소가 오름차순 또는 내림차순으로 정렬된 배열에서 검색하는 알고리즘이다.
이진 검색은 선형 검색보다 좀 더 빠르게 검색할 수 있다는 장점이 있다.
- 이진 검색을 한 단계씩 진행할 때마다 검색 범위가 (거의) 반으로 좁혀진다.
- 요소를 하나씩 제외시키는 선형 검색과는 다르게 이진 검색은 검색할 요소가 해당 단계에서 다음에 검색할 범위의 중간 지점으로 단숨에 이동한다.

이진 검색하기

오름차순으로 정렬된 배열 a의 데이터에서 35를 검색한다.
검색 범위의 맨 앞 인덱스를 pl, 맨 끝 인덱스를 pr, 중앙 인덱스를 pc라고 지정한다. 검색을 시작할 때 pl은 0, pr은 n - 1, pc는 (n - 1) / 2로 초기화한다.

이진 검색

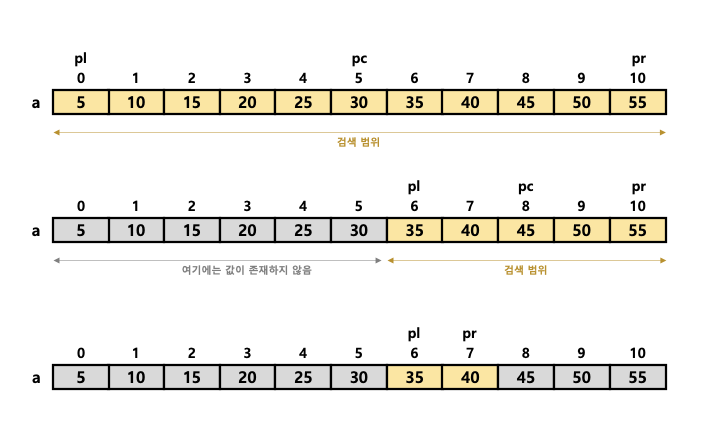
오름차순으로 정렬된 데이터에서 검색을 할 때, 먼저 배열의 중앙에 위치한 a[5] 요소부터 검색을 시작한다. 중앙에 위치한 요소가 원하는 값인지 확인하고, 검색하려는 값보다 큰지 작은지 판단한다. 그리고 검색 대상을 앞쪽이나 뒤쪽으로 좁힌다. 또다시 두 중앙 요소를 선택하고 검색 범위를 좁혀 나간다.
a[pc] < key일 때
- a[pl] ~ a[pc]는 key보다 작은 것이 분명하므로 검색 대상에서 제외한다.
- 검색 범위는 중앙 요소 a[pc]보다 뒤쪽의 a[pc + 1] ~ a[pr]로 좁힌다.
- 그런 다음 pl의 값을 pc + 1로 업데이트 한다.
a[pc] > key일 때
- a[pc] ~ a[pr]은 key보다 큰 것이 분명하므로 검색 대상에서 제외한다.
- 검색 범위는 중앙 요소 a[pc]보다 앞쪽 a[pl] ~ a[pc - 1]로 좁힌다.
- 그런 다음 pr의 값을 pc-1로 업데이트한다.
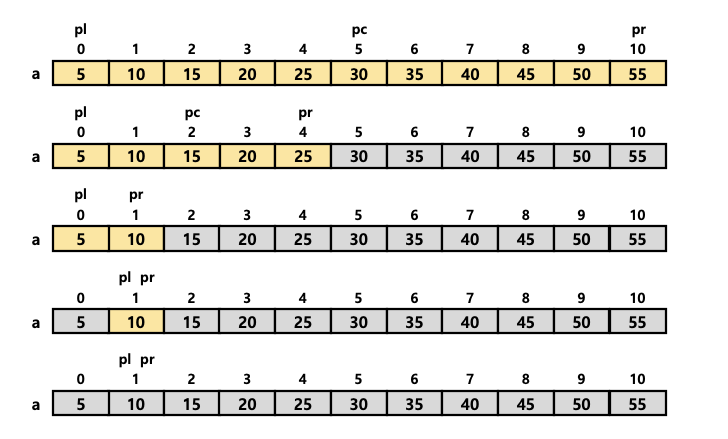
이진 알고리즘의 종료 조건
- 조건1) a[pc]와 key가 일치하는 경우 (검색 성공)
- 조건2) 검색 범위가 더 이상 없는 경우 (검색 실패)
원하는 값을 찾지 못했는데, 검색 범위가 더이상 없을 경우 검색에 실패하기도 한다.
배열 a에서 6을 검색하려고 하는데, 배열 a의 데이터에는 6은 존재하지 않는다. 검색 범위를 좁혀가며 검색을 하는데, pl이 pr보다 커지면서 검색 범위를 더이상 계산할 수 없게 된다. 종료 조건 2가 성립하므로 검색에 실패한다.

이진 검색

이진 검색은 검색을 반복할 때마다 검색 범위가 절반이 되므로 검색애 필요한 비교 횟수의 평균 값은 log n이다. 검색에 실패한 경우는 log(n+1)회(크거나 같으면거 가장 작은 정수), 검색에 성공한 경우는 대략 log n - 1회이다.
이진 검색 알고리즘은 검색 대상(배열)이 정렬(sort)되어 있음을 가정한다. 따라서 이 프로그램에서는 배열의 각 요소의 값을 입력하는 과정에서 바로 앞에 입력한 요소보다 작은 값인 경우에는 다시 입력하게 한다.

package chapter03;

import java.util.Scanner;

public class ex03 {
  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);

    System.out.print("요솟수 : ");
    int no = stdIn.nextInt();
    int[] x = new int[no]; // 요솟수가 no인 배열 생성

    System.out.println("오름 차순으로 입력하세요.");

    System.out.printf("x[0] : ");
    x[0] = stdIn.nextInt();

    for (int i = 1; i < no; i++) {
      do {
        System.out.printf("x[%d] : ", i);
        x[i] = stdIn.nextInt();
      } while (x[i] < x[i - 1]); // 바로 앞의 요소보다 작으면 다시 입력
    }

    System.out.print("검색할 값(숫자) : ");
    int key = stdIn.nextInt();

    int index = binSearch(x, no, key); // 배열 x에서 키 값이 key인 요소 검색
    
    if (index == -1) {
      System.out.println("검색에 실패했습니다.");

    } else {
      System.out.printf("%d는 %d번째 요소입니다.", key, index);
    }

  }

  static int binSearch(int[] a, int n, int key) {
    int pl = 0; // 검색 범위의 첫 인덱스
    int pr = n - 1; // 검색 범위의 끝 인덱스

    do {
      int pc = (pl + pr) / 2; // 중앙 요소의 인덱스
      if (a[pc] == key) {
        return pc; // 검색 성공
      } else if (a[pc] < key) {
        pl = pc + 1; // 검색 범위를 뒤쪽으로 좁힘
      } else {
        pr = pc - 1; // 검색 범위를 앞쪽으로 좁힘
      }
    } while (pl <= pr);

    return -1; // 검색 실패
  }

}

(2) 복잡도

프로그램의 실행 속도는 프로그램이 동작하는 하드웨어나 컴파일러 등의 조건에 따라 달라진다. 알고리즘 성능을 객관적으로 평가하는 기준을 복잡도(complexity)라 한다.
- 시간 복잡도(time complexity) : 실행에 필요한 시간을 평가한 것
- 공간 복잡도(space complexity) : 기억 영역과 파일 공간이 얼마나 필요한가를 평가한 것

선형 검색의 시간 복잡도

static int seqSearch(int[] a, int n, int key) {
  int i = 0; // ①
  while (i < n) { // ②
    if (a[i] == key) { // ③
      return i; // **④**
    }
    i++; // ⑤
  }
	return -1; // ⑥
}

변수 i에 0을 대입(①)하는 횟수는 처음 한 번 실행한 이후에는 없다. 이렇게 한 번만 실행하는 경우 복잡도는 O(1)로 표기한다.
메서드의 값을 반환하는 ④와 ⑥도 한 번만 실행하기 때문에 O(1)로 표기한다.
배열의 맨 끝에 도달했는지를 판단하는 ②와 현재 검사하고 있는 요소와 찾고자 하는 값이 같은지를 판단하는 ③의 평균 실행 횟수는 n/2이다. 이처럼 n에 비례하는 횟수만큼 실행하는 경우의 복잡도를 O(n)으로 표기한다.
n/2번 실행했을 때 복잡도를 O(n/2)가 아닌 O(n)으로 표현하는 이유는 n의 값이 무한히 커진다고 가정했을 때, 그 값의 차이가 무의미해지기 때문이다. 마찬가지로 100번만 실행하는 경우에도 O(100)이 아닌 O(1)로 표기한다. 컴퓨터에 100번을 계산하는 시간과 1번만 계산하는 시간의 차이는 사람이 느낄 수 없을 정도로 굉장히 작다.
복잡도를 표기할 때 사용하는 O는 Order에서 따온 것으로, O(n)은 'O - n', 'Order n', 'n의 Order'라고 읽는다.

단계	실행 횟수	복잡도
①	1	O(1)
②	n/2	O(n)
③	n/2	O(n)
④	1	O(1)
⑤	n/2	O(n)
⑥	1	O(1)

n이 점점 커지면 O(n)에 필요한 계산 시간은 n에 비례하여 점점 길어진다. 이와 달리 O(1)에 필요한 계산 시간은 변하지 않는다.
일반적으로 O(f(n))과 O(g(n))의 복잡도를 계산하는 방법은 아래와 같다.

O(f(n)) + O(g(n)) = O(max(f(n), g(n))) // max(a, b)는 a와 b 가운데 큰 쪽을 나타내는 메서드

2개 이상의 복잡도로 구성된 알고리즘의 전체 복잡도는 차원이 가장 높은 복잡도를 선택한다. 둘이 아니라 셋 이상의 계산으로 구성된 알고리즘도 마찬가지이다.

O(1) + O(n) + O(n) + O(1) + O(n) + O(1) = O(max(1, n, n, 1, n, 1)) = O(n)

연습 문제

Q1) ex02의 seqSearchSen 메서드를 while문이 아니라 for문을 사용하여 수정한 프로그램을 작성하세요.

// 나의 풀이
static int seqSearchSen(int[] a, int n, int key) {
  a[n] = key; // 보초 추가

  for (int i = 0; i <= n; i++) {
    if (a[i] == key) { // 검색 성공
      return i;
    }
  }
  return -1;
}

// 해설
static int seqSearchSen(int[] a, int n, int key) {
  int i;

  a[n] = key; // 보초를 추가

  for (i = 0; a[i] != key; i++)
    ;
  return i == n ? -1 : i;
}

Q2) 선형 검색의 스캐닝 과정을 상세하게 출력하는 프로그램을 작성하세요. 이때 각 행의 맨 왼쪽에 현재 검색하는 요소의 인덱스를 출력하고, 현재 검색하고 있는 요소 위에 별표 기호 *를 출력하세요.

package chapter03;

import java.util.Scanner;

public class quiz02 {
  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);

    System.out.print("요솟수 : ");
    int no = stdIn.nextInt();
    int[] x = new int[no]; // 요솟수가 no인 배열 생성

    for (int i = 0; i < no; i++) {
      System.out.printf("x[%d] : ", i);
      x[i] = stdIn.nextInt();
    }

    System.out.print("검색할 값(숫자) : ");
    int key = stdIn.nextInt();

    int index = seqSearchEx(x, no, key); // 배열 x에서 키 값이 key인 요소 검색

    if (index == -1) {
      System.out.println("검색에 실패했습니다.");

    } else {
      System.out.printf("%d는 %d번째 요소입니다.", key, index);
    }

  }

  static int seqSearchEx(int[] a, int n, int key) {
    System.out.print("   |");
    for (int k = 0; k < n; k++) {
      System.out.printf("%4d", k);
    }
    System.out.println();

    System.out.print("---+");
    for (int k = 0; k < 4 * n + 2; k++) {
      System.out.print("-");
    }
    System.out.println();

    for (int i = 0; i < n; i++) {
      System.out.print("   |");
      System.out.printf(String.format("%%%ds*\n", (i * 4) + 3), "");
      System.out.printf("%3d|", i);
      for (int k = 0; k < n; k++) {
        System.out.printf("%4d", a[k]);
      }
      System.out.println("\n   |");
      if (a[i] == key) {
        return i; // 검색 성공
      }
    }
    return -1; // 검색 실패
  }

}

요솟수 : 3
x[0] : 1
x[1] : 2
x[2] : 3
검색할 값(숫자) : 4
   |   0   1   2
---+--------------
   |   *
  0|   1   2   3
   |
   |       *
  1|   1   2   3
   |
   |           *
  2|   1   2   3
   |
검색에 실패했습니다.

이진 검색의 시간 복잡도

이진 검색법을 이용하면 검색할 요소의 범위를 절반씩 좁힐 수 있다.

static int binSearch(int[] a, int n, int key) {
  int pl = 0; // ①
  int pr = n - 1; // ②

  do {
    int pc = (pl + pr) / 2; // ③
    if (a[pc] == key) { // ④
      return pc; // ⑤
    } else if (a[pc] < key) { // ⑥
      pl = pc + 1; // ⑦
    } else {
      pr = pc - 1; // ⑧
    }
  } while (pl <= pr); // ⑨

  return -1; // ⑩
}

프로그램 각 단계의 실행 횟수와 복잡도는 다음과 같다.

단계	실행 횟수	복잡도
①	1	O(1)
②	1	O(1)
③	log n	O(log n)
④	log n	O(log n)
⑤	1	O(1)
⑥	log n	O(log n)
⑦	log n	O(log n)
⑧	log n	O(log n)
⑨	log n	O(log n)
⑩	1	O(1)

이진 검색 알고리즘의 복잡도를 구하면 아래처럼 O(log n)을 얻을 수 있다.

O(1) + O(1) + O(log n) + O(log n) + O(1) + O(log n) + ... + O(1) = O(log n)

그런데 O(n)과 O(log n)은 O(1) 보다 크다.

연습 문제

Q3) 요솟수가 n인 배열 a에서 key와 일치하는 모든 요소의 인덱스를 배열 idx의 맨 앞부터 순서대로 저장하고, 일치한 요솟수를 반환하는 메서드를 작성하세요. 예를 들어 요솟수가 8인 배열 a의 요소가 {1, 9, 2, 9, 4, 6, 7, 9}이고 key가 9면 배열 idx에 {1, 3, 7}을 가정하고 3을 반환합니다.

package chapter03;

import java.util.Scanner;

public class quiz {
  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);

    System.out.print("요솟수 : ");
    int no = stdIn.nextInt();
    int[] x = new int[no]; // 요솟수가 no인 배열 생성
    int[] index = new int[no]; // 요솟수가 no인 배열 생성

    for (int i = 0; i < no; i++) {
      System.out.printf("x[%d] : ", i);
      x[i] = stdIn.nextInt();
    }

    System.out.print("검색할 값(숫자) : ");
    int key = stdIn.nextInt();

    int count = seqSearchIndex(x, no, key, index); // 배열 x에서 키 값이 key인 요소 검색

    if (count == 0) {
      System.out.println("검색에 실패했습니다.");

    } else {
      for (int i = 0; i < count; i++) {
        if (index[i] != 0) {
          System.out.printf("%d는 x[%d]에 있습니다. \n",key, index[i]);
        }
      }
    }

  }

	// 배열 a의 앞쪽 n개 요소에서 key와 같은 모든 요소의 index를
	// 배열idx의 머리부터 차례로 저장하여 같은 요솟수를 반환하는 메서드
  static int seqSearchIndex(int[] a, int n, int key, int[] index) {
    int count = 0;
    for(int i = 0; i < n; i++) {
      if (a[i] == key) {
        index[count++] = i;
      }
    }
    return count;
  }

}

Q4) 이진 검색의 과정을 출력하는 프로그램을 작성하세요. 각 행의 맨 왼쪽에 현재 검색하고 있는 요소의 인덱스를 출력하고, 검색 범위의 맨 앞 요소 위에 <-, 맨 끝 요소 위에 ->, 현재 검색하고 있는 중앙 요소 위에 +를 출력하도록 하세요.

package chapter03;

import java.util.Scanner;

public class quiz04 {
  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);

    System.out.print("요솟수 : ");
    int no = stdIn.nextInt();
    int[] x = new int[no]; // 요솟수가 no인 배열 생성

    for (int i = 0; i < no; i++) {
      System.out.printf("x[%d] : ", i);
      x[i] = stdIn.nextInt();
    }

    System.out.print("검색할 값(숫자) : ");
    int key = stdIn.nextInt();

    int index = binSearchX(x, no, key); // 배열 x에서 키 값이 key인 요소 검색

    if (index == -1) {
      System.out.println("검색에 실패했습니다.");

    } else {
      System.out.printf("%d는 %d번째 요소입니다.", key, index);
    }

  }

  static int binSearchX(int[] a, int n, int key) {
    System.out.print("   |");
    for(int i = 0; i < a.length; i++) {
      System.out.printf("%4d", a[i]);
    }
    System.out.println();

    System.out.print("---+");
    for(int i = 0; i < a.length; i++) {
      System.out.print("----");
    }
    System.out.println();

    int pl = 0; // 검색 범위의 첫 인덱스
    int pr = n - 1; // 검색 범위의 끝 인덱스

    do {
      int pc = (pl + pr) / 2; // 중앙 요소의 인덱스

      System.out.print("   |");
      if (pl != pc)
          System.out.printf(String.format("%%%ds<-%%%ds+", (pl * 4) + 1, (pc - pl) * 4), "", "");
      else
          System.out.printf(String.format("%%%ds<-+", pc * 4 + 1), "");
      if (pc != pr)
          System.out.printf(String.format("%%%ds->\n", (pr - pc) * 4 - 2), "");
      else
          System.out.println("->");

      System.out.printf("%3d|", pc);
      for (int k = 0; k < n; k++)
          System.out.printf("%4d", a[k]);
      System.out.println("\n   |");

      if (a[pc] == key) {
        return pc;

      } else if (a[pc] < key) {
        pl = pc + 1; // 검색 범위를 뒤쪽으로 좁힘
      } else {
        pr = pc - 1; // 검색 범위를 앞쪽으로 좁힘
      }
    } while (pl <= pr);

    return -1; // 검색 실패
  }

}

요솟수 : 7
x[0] : 2
x[1] : 4
x[2] : 3
x[3] : 6
x[4] : 3
x[5] : 5
x[6] : 1
검색할 값(숫자) : 4
   |   2   4   3   6   3   5   1
---+----------------------------
   | <-            +          ->
  3|   2   4   3   6   3   5   1
   |
   | <-    +  ->
  1|   2   4   3   6   3   5   1
   |
4는 1번째 요소입니다.

Q5) 우리가 살펴본 이진 검색 알고리즘 프로그램은 검색할 값과 같은 값을 갖는 요소가 하나 이상일 경우 그 요소 중에서 맨 앞의 요소를 찾지 못한다. 맨 앞의 요소를 찾는 binSearchX 메서드를 작성해보세요. (이진 검색 알고리즘에 의해 검색에 성공했을 때 그 위치로부터 앞쪽으로 하나씩 검사하면 여러 요소가 일치하는 경우에도 가장 앞쪽에 위치하는 요소의 인덱스를 찾아냅니다.)

// 나의 풀이
static int binSearchX(int[] a, int n, int key) {
  int pl = 0; // 검색 범위의 첫 인덱스
  int pr = n - 1; // 검색 범위의 끝 인덱스

  do {
    int pc = (pl + pr) / 2; // 중앙 요소의 인덱스
    if (a[pc] == key) {
      for (int i = 0; i < pr; i++) {
        if (a[i] == key) {
          return i;
        }
      }
      return pc;

    } else if (a[pc] < key) {
      pl = pc + 1; // 검색 범위를 뒤쪽으로 좁힘
    } else {
      pr = pc - 1; // 검색 범위를 앞쪽으로 좁힘
    }
  } while (pl <= pr);

  return -1; // 검색 실패
}

// 해설
static int binSearchX(int[] a, int n, int key) {
  int pl = 0; // 검색범위 맨 앞의 index
  int pr = n - 1; // 검색범위 맨 뒤의 index

  do {
    int pc = (pl + pr) / 2; // 중앙요소의 index
    if (a[pc] == key) {
      for (; pc > pl; pc--) // key와 같은 맨 앞의 요소를 찾습니다
        if (a[pc - 1] < key)
          break;
        return pc; // 검색 성공
      } else if (a[pc] < key)
          pl = pc + 1; // 검색범위를 앞쪽 절반으로 좁힘
      else
        pr = pc - 1; // 검색범위를 뒤쪽 절반으로 좁힘
    } while (pl <= pr);

    return -1; // 검색 실패
}

나의 풀이는, 이진 검색의 장점을 살리지 못했다. 중앙 요소와 key값이 같을 경우 중앙 요소 앞쪽의 모든 값을 일일이 검사하여 key값과 일치하는 요소가 있는지 확인한다. 효율적이지 못하다. 해설에서는 key값과 같은 맨 앞의 요소를 찾을 때, pc의 값을 줄여나가며 이진 검색을 수행한다.

(3) Arrays.binarySearch에 의한 이진 검색

Java는 배열에서 이진 검색을 하는 메서드를 표준 라이브러리로 제공한다. 이진 검색 표준 라이브러리의 메서드로는 java.util.Arrays 클래스의 binarySearch 메서드가 있다.
binarySearch 메서드는 다음과 같은 장점이 있다.
- 장점1) 이진 검색 메서드를 직접 코딩할 필요가 없다.
- 장점2) 모든 자료형 배열에서 검색할 수 있다.
API 문서란, 라이브러리를 사용하는 방법을 작성해 놓은 것이다. Java API 공식 문서는 "http://docs.oracle.com/javase/8/docs/api/"에 접속하면 찾을 수 있다. 예를 들어 binarySearch 메서드에 대한 설명을 찾으려면 Array 클래스를 먼저 왼쪽 목록에서 찾고 그런 다음에 binarySearch 메서드에 대한 설명을 찾으면 된다.
binarySearch 메서드는 오름차순으로 정렬된 a를 가정하고, 키 값이 key인 요소를 이진 검색한다. binarySearch 메서드는 자료형에 따라 9가지 방법으로 오버로딩(overloading)되어 있다.

static int binarySearch(byte[] a, byte key)
static int binarySearch(char[] a, char key)
static int binarySearch(double[] a, double key)
static int binarySearch(float[] a, float key)
static int binarySearch(int[] a, int key)
static int binarySearch(long[] a, long key)
static int binarySearch(short[] a, short key)
static int binarySearch(Object[] a, Object key)
static <T> binarySearch(T[] a, Comparator<? super T> key)

검색에 성공한 경우

key와 일치하는 요소의 인덱스를 반환한다.
일치하는 요소가 여러 개 있다면 무작위의 인덱스를 반환한다. 맨 앞의 인덱스나 어떤 특정한 인덱스를 반환하는 것이 아니다.

검색에 실패한 경우

반환값은 삽입 포인트를 x라고 할 때 -x - 1을 반환한다.
삽입 포인트는 검색하기 위해 지정한 key보다 큰 요소 중 첫 번째 요소의 인덱스이다. 만약 배열의 모든 요소가 key보다 작다면 배열의 길이를 삽입 포인트로 정한다.
예를 들어 아래의 배열에서 key가 4이라면, 4보다 큰 요소 중 첫 번째 요소의 인덱스가 3이므로, 삽입 포인트는 3이다. 즉 , -4를 반환한다.

이진 검색

배열 {5, 7, 15, 28, 29, 31, 39, 58, 68, 70}에서 binarySearch 메서드를 검색하는 여러 경우를 나타내 보았다.

이진 검색

39 검색 : 검색 성공, 해당 인덱스(6)를 반환한다.
30 검색 : 검색 실패, 삽입 포인트는 5이고 -6을 반환한다.
95 검색 : 검색 실패, 모든 요소가 검색하는 값보다 작기 때문에 삽입 포인트는 10이고, -11을 반환한다.

기본 자료형 배열에서 binarySearch 메서드로 검색하기

binarySearch 메서드는 int형이나 long형과 같은 기본 자료형 배열에서 이진 검색을 하는 메서드이다.
int형 배열에서 이 메서드를 사용하는 방법은 다음과 같다.

package chapter03;

import java.util.Arrays;
import java.util.Scanner;

public class ex04 {
  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);

    System.out.print("요솟수 : ");
    int no = stdIn.nextInt();
    int[] x = new int[no]; // 요솟수가 no인 배열 생성

    System.out.println("오름 차순으로 입력하세요.");

    System.out.printf("x[0] : ");
    x[0] = stdIn.nextInt();

    for (int i = 1; i < no; i++) {
      do {
        System.out.printf("x[%d] : ", i);
        x[i] = stdIn.nextInt();
      } while (x[i] < x[i - 1]); // 바로 앞의 요소보다 작으면 다시 입력
    }

    System.out.print("검색할 값(숫자) : ");
    int key = stdIn.nextInt();

    int index = Arrays.binarySearch(x, key); // 배열 x에서 키 값이 key인 요소 검색

    if (index < 0 ) {
      System.out.println("검색에 실패했습니다.");

    } else {
      System.out.printf("%d는 %d번째 요소입니다.", key, index);
    }
  }
}

Arrays.binarySearch(x, key); 에서 배열 x와 키 값인 key를 전달하면, 컴파일러가 자동으로 호출하는 메서드를 결정한다. 메서드를 사용하는 개발자가 지정하지 않아도 된다.

연습 문제

Q6) ex04를 수정하여 검색에 실패하면 삽입 포인트의 값을 출력하는 프로그램을 작성하세요.

package chapter03;

import java.util.Arrays;
import java.util.Scanner;

public class quiz06 {
  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);

    System.out.print("요솟수 : ");
    int no = stdIn.nextInt();
    int[] x = new int[no]; // 요솟수가 no인 배열 생성

    System.out.println("오름 차순으로 입력하세요.");

    System.out.printf("x[0] : ");
    x[0] = stdIn.nextInt();

    for (int i = 1; i < no; i++) {
      do {
        System.out.printf("x[%d] : ", i);
        x[i] = stdIn.nextInt();
      } while (x[i] < x[i - 1]); // 바로 앞의 요소보다 작으면 다시 입력
    }

    System.out.print("검색할 값(숫자) : ");
    int key = stdIn.nextInt();

    int index = Arrays.binarySearch(x, key); // 배열 x에서 키 값이 key인 요소 검색

    if (index < 0 ) {
      System.out.println("검색에 실패했습니다.");
      System.out.printf("삽입 포인트는 %d입니다.\n", - index - 1);

    } else {
      System.out.printf("%d는 %d번째 요소입니다.", key, index);
    }
  }
}

요솟수 : 3
오름 차순으로 입력하세요.
x[0] : 1
x[1] : 3
x[2] : 5
검색할 값(숫자) : 2
검색에 실패했습니다.
삽입 포인트는 1입니다.

클래스 메서드와 인스턴스 메서드

Java 메서드의 종류는 인스턴스 메서드(비정적 메서드), 클래스 메서드(정적 메서드) 두 가지이다.
인스턴스 메서드는 static을 붙이지 않고 선언한 메서드이고, 클래스 메서드는 static을 붙여 선언한 메서드이다. 둘의 차이점은 ‘메서드가 인스턴스에 포함되는지‘의 여부에 있다.
클래스 메서드는 클래스 전체에 대한 처리를 담당하며 인스턴스 메서드와 처리 영역을 구분하기 위해 주로 사용한다.

package chapter03;

class Id{
  private static int counter = 0; // 아이디를 몇 개 부여했는지 저장
  private int id;

  public Id() {
    id = ++counter;
  }

  public int getId() {
    return id;
  }

  public static int getCounter() {
    return counter;
  }
}

public class ex06 {
  public static void main(String[] args) {
    Id a = new Id();
    Id b = new Id();

    System.out.println("a의 아이디 : " + a.getId());
    System.out.println("b의 아이디 : " + b.getId());

    System.out.println("부여한 아이디의 개수 : " + Id.getCounter());
  }
}

클래스 메서드와 마찬가지로 클래스 변수도 인스턴스에 포함되지 않는다. 또한 인스턴스의 개수와 관계없이 1개만 만들어진다.
인스턴스 메서드와 클래스 메서드는 호출하는 방식이 다르다.
- 인스턴스 메서드 호출시 : 클래스형 변수 이름.메서드 이름
- 클래스 메서드 호출시 : 클래스 이름.메서드 이름

객체의 배열에서 검색하기

static int binarySearch(Object[] a, Object key)
- 자연 정렬이라는 방법으로 요소의 대소 관계를 판단한다. 따라서 정수 배열, 문자열 배열에서 검색할 때 적당하다.
**static binarySearch(T[] a, T key, Comparator<? super T> c)**
- “자연 순서”가 아닌 순서로 줄지어 있는 배열을 검색하거나 “자연 순서”를 논리적으로 갖지 않늕 클래스 배열에서 검색할 때 알맞다.

자연 정렬(natural ordering)

binarySearch 메더스에 배열과 키 값을 전달하는 간단한 방법으로 검색할 수 있는 이유는 String 클래스가 Comparable 인터페이스와 compareTo 메서드를 구현하고 있기 때문이다.

문자열 정렬	자연 정렬
텍스트1.txt	텍스트1.txt
텍스트10.txt	텍스트2.txt
텍스트100.txt	텍스트10.txt
텍스트2.txt	텍스트21.txt
텍스트21.txt	텍스트100.txt

문자열 정렬은 말 그대로 동일한 위치에 있는 문자의 대소 비교를 통해 정렬하는데, 사람이 보기에는 자연스럽지 않다. 사람에게는 오른쪽의 정렬이 더 자연스러운데, 이 정렬을 ‘자연 정렬‘이라 부른다.

class A implements Comparable<A> { // Comparable<A> 인터페이스 구현

	public int compareTo(A c) { // compareTo 메서드 구현
		// this가 c보다 크면 양의 값 반환
		// this가 c보다 작으면 음의 값 반환
		// this와 c가 같으면 0 반환
	}

	public boolean equals(Object c) { // equals 메서드 구현
		// this가 c와 같으면 true 반환
		// this갸 c와 같지 않으면 false 반환
	}

}

자연 정렬로 정렬된 배열에서 메서드 검색하기

static int binarySearch(Object[] a, Object key)

자연 정렬에서 대소 관계를 비교하는 메서드를 사용하여 검색하는 프로그램을 작성한다. 검색 대상인 x는 문자열 배열이고, 문자열을 key에 입력하고 배열 x와 키 값 key를 binarySearch메서드에 전달하면 검색할 수 있다.

package chapter03;

import java.util.Arrays;
import java.util.Scanner;

public class ex07 {
  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);

    String[] x = {
        "abstract",   "assert",       "boolean",   "break",      "byte",
        "case",       "catch",        "char",      "class",      "const",
        "continue",   "default",      "do",        "double",     "else",
        "enum",       "extends",      "final",     "finally",    "float",
        "for",        "goto",         "if",        "implements", "import",
        "instanceof", "int",          "interface", "long",       "native",
        "new",        "package",      "private",   "protected",  "public",
        "return",     "short",        "static",    "strictfp",   "super",
        "switch",     "synchronized", "this",      "throw",      "throws",
        "transient",  "try",          "void",      "volatile",   "while"
    };

    System.out.print("키워드를 입력하세요 : "); // 키 값 입력
    String key = stdIn.next();

    int index = Arrays.binarySearch(x, key);

    if (index < 0) {
      System.out.println("해당 키워드가 없습니다.");
    } else {
      System.out.printf("해당 키워드는 x[%d]에 있습니다.\n", index);
    }
  }
}

binarySearch 메서드가 전달받는 자료형은 Object이다. Object는 모든 클래스의 상위 클래스이다. 그래서 어떤 형태의 클래스도 받을 수 있다.

자연 정렬로 정렬되지 않은 배열에서 검색하기

**static binarySearch(T[] a, T key, Comparator<? super T> c)**

자연 정렬로 정렬되지 않은 배열에서의 검색은 제네릭 메서드(generic method)로 하면 된다.
제네릭 메서드의 첫 번재 매개변수 a는 검색 대상이고, 두 번째 매개변수 key는 키 값이다. 제네릭 메서드는 자료형에 구애받지 않는다. 따라서 매개변수로 전달하는 자료형은 Integer, String, 신체검사 데이터용 클래스 PhyscData 등 어떤 것을 전달해도 된다.
하지만 배열의 요소가 어떤 순서로 줄지어 있는지, 각 요소의 대소 관계를 어떻게 판단할 것인지에 대해서는 binarySearch 메서드에 알려줘야 한다. 이 정보는 세 번째 매개변수 c에 전달한다.
Comparator<? super T> c
- 클래스 T(또는 클래스 T의 슈퍼클래스)로 생성한 두 객체의 대소 관계를 판단하기 위한 comparator이다. comparator 안에는 compare 메서드가 있다.

package java.util;

// java.util.Comparator 인터페이스
public interface Comparator <T> {
	int compare(T o1, T o2);
	boolean equals(Object obj);
}

객체의 대소관계를 판단하는 comparator를 직접 구현하려면 Comparator 인터페이스를 구현한 클래스를 정의하고 그 클래스의 인스턴스를 생성해야 한다. 그 다음 매개변수로 전달된 두 객체의 대소 관계를 비교하여 그 결과를 반환하는 compare 메서드를 구현하면 된다.

public int compare(T d1, T d2) {
	if(d1 > d2) return 양수;
	if(d1 < d2) return 음수;
	if(d1 == d2) return 0;
}

클래스의 내부에서 comparator를 정의하는 방법은 다음과 같다. Comparator 인터페이스와 compare 메서드를 구현한 클래스를 먼저 작성하고, 그 후 클래스의 인스턴스를 생성한다. 아래의 코드에서는 comparator를 클래스 내부에서 정의하고 있지만, 클래스 외부에서 정의해도 된다.

package chapter03;

import java.util.Comparator;

class X {
  public static final Comparator<T> COMPARATOR = new Comp();

  private static class Comp implements Comparator<T> {
    public int compare(T d1, T d2) {
      // d1이 d2보다 크면 양의 값 반환
      // d1이 d2보다 작으면 음의 값 반환
      // d1이 d2와 같으면 0 반환
    }
  }
}

comparator를 사용하기 위해서는, binarySearch 메서드의 세 번째 매개변수로 클래스 X의 클래스 변수인 X.COMPARATOR를 전달하면 된다. 호출된 binarySearch 메서드는 전달받은 comparator를 기준으로 배열 요소의 대소 관계를 판단하여 이진 검색을 수행한다.
키 순서대로 정렬된 신체검사 데이터의 배열에서 특정한 사람의 키를 검색하는 프로그램을 작성하는데, comparator를 사용한다.

package chapter03;

import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;

public class ex08 {

  static class PhyscData {
    private String name;
    private int height;
    private double vision;

    public PhyscData(String name, int height, double vision) {
      this.name = name;
      this.height = height;
      this.vision = vision;
    }

    @Override
    public String toString() {
      return name + " " + height + " " + vision;
    }

    // 키 순서대로 (오름차순) 데이터를 정렬하기 위한 comparator
    public static final Comparator<PhyscData> HEIGHT_ORDER = new HeightOrderComparator();

    private static class HeightOrderComparator implements Comparator<PhyscData> {
      @Override
      public int compare(PhyscData d1, PhyscData d2) {
        return (d1.height > d2.height) ? 1 :
               (d1.height < d2.height) ? -1 : 0;
      }
    }
  }

  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);
    PhyscData[] x = {
        new PhyscData("정현희", 162, 0.3),
        new PhyscData("유지연", 168, 0.4),
        new PhyscData("김두나", 169, 0.8),
        new PhyscData("홍준기", 171, 1.5),
        new PhyscData("전서현", 173, 0.7),
        new PhyscData("이호연", 174, 1.2),
        new PhyscData("김인호", 175, 2.0),
    };

    System.out.print("키가 몇 cm인 사람을 찾나요? ");
    int height = stdIn.nextInt();

    int index = Arrays.binarySearch(
        x,                                  // 배열 x에서
        new PhyscData("", height, 0.0),     // 키가 height인 요소를
        PhyscData.HEIGHT_ORDER              // HEIGHT_ORDER에 의해 검색
    );

    if (index < 0) {
      System.out.println("찾는 데이터가 없습니다.");
    } else {
      System.out.printf("x[%d]에 있습니다.\n", index);
      System.out.println("찾은 데이터 : " + x[index]);
    }
  }
}

키가 몇 cm인 사람을 찾나요? 168
x[1]에 있습니다.
찾은 데이터 : 유지연 168 0.4

연습 문제

Q7) 시력에 대한 내림차순 정렬의 신체검사 데이터에서 특정 시력을 가진 사람을 검색하는 프로그램을 작성하세요.

package chapter03;

import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;

public class quiz07 {

  static class PhyscData {
    private String name;
    private int height;
    private double vision;

    public PhyscData(String name, int height, double vision) {
      this.name = name;
      this.height = height;
      this.vision = vision;
    }

    @Override
    public String toString() {
      return name + " " + height + " " + vision;
    }

    // 시력 순서대로 (내림차순) 데이터를 정렬하기 위한 comparator
    public static final Comparator<PhyscData> VISION_ORDER = new VisionOrderComparator();

    private static class VisionOrderComparator implements Comparator<PhyscData> {
      @Override
      public int compare(PhyscData d1, PhyscData d2) {
        return (d1.vision > d2.vision) ? 1 :
               (d1.vision < d2.vision) ? -1 : 0;
      }
    }
  }

  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);
    PhyscData[] x = {
        new PhyscData("정현희", 162, 0.3),
        new PhyscData("유지연", 168, 0.4),
        new PhyscData("김두나", 169, 0.8),
        new PhyscData("홍준기", 171, 1.5),
        new PhyscData("전서현", 173, 0.7),
        new PhyscData("이호연", 174, 1.2),
        new PhyscData("김인호", 175, 2.0),
    };

    System.out.print("시력이 얼마인 사람을 찾나요? ");
    double vision = stdIn.nextDouble();

    int index = Arrays.binarySearch(
        x, 
        new PhyscData("", 0, vision), 
        PhyscData.VISION_ORDER
    );

    if (index < 0) {
      System.out.println("찾는 데이터가 없습니다.");
    } else {
      System.out.printf("x[%d]에 있습니다.\n", index);
      System.out.println("찾은 데이터 : " + x[index]);
    }
  }
}

시력이 얼마인 사람을 찾나요? 2.0
x[6]에 있습니다.
찾은 데이터 : 김인호 175 2.0

제네릭

제네릭은 처리해야 할 대상의 자료형에 의존하지 않는 클래스(인터페이스) 구현 방식이다. 제네릭 클래스는 자료형에 의존하지 않기 때문에 범용으로 사용할 수 있다.
제네릭 클래스는 클래스 이름 바로 뒤에 <Type> 같은 형식의 파라미터를 붙여 선언한다. 이렇게 정의된 클래스나 인터페이스는 매개변수로 정의한 ‘자료형’을 전달받을 수 있다.

class     클래스 이름    <파라미터> { }
interface 인터페이스 이름 <파라미터> { }

파라미터를 쉼표로 구분하면 파라미터를 여러 개 지정할 수 있다.

class     클래스 이름    <파라미터1, 파라미터2, ...> { }
interface 인터페이스 이름 <파라미터1, 파라미터2, ...> { }

파라미터 이름을 작성하는 방법
- 1개의 대문자를 사용한다(소문자는 가급적 사용하지 않는다).
- 컬렉션(collection)의 자료형은 element의 앞글자인 E를 사용한다.
- 맵(Map), 키(key), 값(value)은 key와 value의 앞글자인 K와 V를 사용한다.
- 일반적으로는 T를 사용한다.
형변수에는 와일드카드를 지정하는 것도 가능하다.

<? extends T> // 클래스 T의 서브 클래스를 전달받는다. 
<? super T> // 클래스 T의 슈퍼 클래스를 전달받는다.

Twitter Facebook LinkedIn

유지연

[Do it! 알고리즘]03. 검색

03-1 검색 알고리즘

(1) 검색과 키

(2) 배열에서 검색하기

03-2 선형 검색

(1) 선형 검색

무한 루프

(2) 보초법

03-2 이진 검색

(1) 이진 검색

이진 검색하기

(2) 복잡도

선형 검색의 시간 복잡도

연습 문제

이진 검색의 시간 복잡도

연습 문제

(3) Arrays.binarySearch에 의한 이진 검색

검색에 성공한 경우

검색에 실패한 경우

기본 자료형 배열에서 binarySearch 메서드로 검색하기

연습 문제

클래스 메서드와 인스턴스 메서드

객체의 배열에서 검색하기

자연 정렬(natural ordering)

자연 정렬로 정렬된 배열에서 메서드 검색하기

자연 정렬로 정렬되지 않은 배열에서 검색하기

연습 문제

제네릭

공유하기

참고

2022-02-22 TIL(at work)

[HTTP] 8. HTTP 헤더2 - 캐시와 조건부 요청

[HTTP] 7. HTTP 헤더1 - 일반 헤더

[HTTP] 6. HTTP 상태 코드